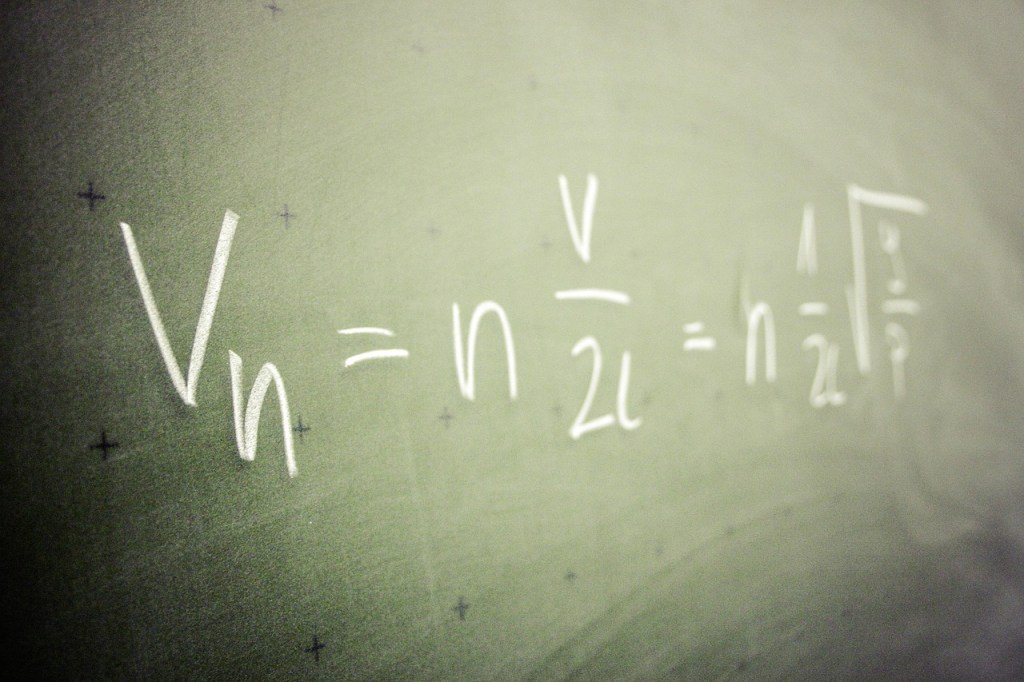
Humanity has always searched for a way to understand reality with clarity. For thousands of years, mathematics has risen as the most reliable language for describing the world around us. It explains how planets move. It reveals the shape of light. It connects the smallest particles with the largest cosmic structures. It does all of this using symbols and rules that fit together with astonishing elegance.
There is a sense of wonder in the idea that numbers and equations can describe events billions of light years away or events so small that they defy any direct observation. Mathematicians and physicists often feel that mathematics is not something humans invented. Instead, it feels discovered, as if the universe itself is written with quantities and relationships waiting for us to notice.
However, the amazing power of mathematics does not mean it is limitless. We encounter points where the language stops. Division by zero gives no valid result. Singularities in physics produce impossible infinities. At the very moment mathematics reveals the depth of our world, it also reveals a boundary. The same system that opens cosmic vistas also shows us where understanding slips beyond the grasp of our symbols. In this contrast, we discover the double role of mathematics. It is a bridge to the unknown and a reminder that some things cannot be fully known.
This duality tells us something important. Mathematics does not define reality. It interprets reality in ways that suit the human mind. The limitations built into the language help us notice places where the world outgrows our concepts. Where mathematics stops, wonder begins.
The Map and the Mountain
Maps are incredibly useful. They guide journeys, reveal hidden routes, and capture the essential structure of territory. Mathematics works like a map of the universe. It gives abstraction to things that we cannot hold in our hands. It removes unnecessary detail to capture the essence of patterns and relationships.
But even the best map is not the mountain. A map can show elevation lines and paths, yet no drawing can capture the feeling of cold air or the struggle of a steep incline. In the same way, mathematics outlines the laws of motion, the symmetry of particles, and the curvature of spacetime. It captures what can be measured and repeated. Yet it cannot tell us how it feels to witness a sunrise or to love someone or to wonder why anything exists at all.
The map is precise. The mountain is real. When the two align perfectly, we celebrate the clarity of science. When the map breaks, it tells us that the mountain has features that have not yet been charted. Black holes are a clear example. Einstein’s equations point toward a place where density becomes infinite and time stops. But a true infinity does not occur in nature as far as we can tell. The mathematics is pointing instead to a blind spot in our understanding of gravity and quantum mechanics.
The failure of mathematics is not a failure of reality. It is a call to refine the map. The mountain always remains.
Beyond One Mathematics
Most of us learn only one style of mathematics as children. We treat its rules as universal truths that apply everywhere. Yet mathematicians know that many different mathematical systems exist. Some allow parallel lines to meet. Others treat time as discrete moments instead of a smooth flow. Some logics tolerate contradiction without collapsing into nonsense.
This variety invites us to think about other kinds of minds. If there are forms of intelligence elsewhere in the universe, their perception of reality might suggest entirely different mathematical structures. What is intuitive to us might appear bizarre to them. What seems impossible to us might be obvious to them. Their mathematics might describe aspects of existence that our own systems never imagined.
This possibility becomes even more interesting when we consider the idea of multiple universes. If other universes exist with different laws of physics, then the mathematics that fits those worlds would differ from ours. Mathematics would not be a single universal structure. It would be a family of systems, each tuned to a particular style of reality.
Still, mathematics would remain a sign of intelligence. A being that discovers patterns and turns them into symbolic systems is engaged in an act that mirrors our own pursuit of understanding. The form might differ. The purpose would be the same. Every mathematics is an attempt to make sense of existence. Every system reveals a way that intelligence meets the world.
Gödel and the Architecture of Incompleteness
No matter how powerful mathematics becomes, there is a built in limit on what any single system of reasoning can accomplish. This principle was made clear by Kurt Gödel in the twentieth century. His incompleteness theorems show that in any consistent mathematical system that can describe ordinary arithmetic, there are true statements that cannot be proven inside that system.
The conclusion is striking. There is no final theory that contains every truth. No matter how advanced a system becomes, it cannot fully explain itself. It relies on axioms that cannot be justified from within. It contains statements whose truth escapes all internal methods of proof. Any attempt to expand the system leads to a new system with new gaps. This ladder has no top rung.
Gödel’s work is often treated as abstract logic. Yet it has a philosophical consequence that reaches much farther. It means that the very project of human understanding contains a structural horizon. We can always go further, but we can never arrive at a complete view from above. There is no position outside the universe from which to understand the universe. There is no place outside the mind from which to observe the mind. The observer and the system remain entangled.
This insight prepares us for a deeper realization. Limits are not temporary obstacles. They are part of the architecture of reality as human reason can grasp it.
The Observer Who Cannot Observe Herself
There is a simple truth we encounter every day. We see the world because our eyes take in light. Yet we cannot see our own eyes directly as they see. We can look in a mirror, but the mirror shows only an image, not the eye at work. The source of seeing cannot fully appear in the field of sight.
This fact is more than a clever observation. It is a metaphor for consciousness. The mind can examine a thought or memory or emotion. It can reflect on part of itself. But the act of awareness itself cannot be aware of itself in the same way. Awareness is the background that makes every object appear. It cannot become an object without losing its role as the source.
This creates a curious situation. We are the beings who can reflect on everything except the foundation of reflection itself. The core of who we are stays just out of reach. We know that we exist. We cannot fully know how existence appears to itself. No concept can capture the one who forms the concept.
The human mind is therefore the greatest example of the limits of mathematical and logical thought. It is both the tool that makes understanding possible and the mystery that remains when understanding reaches its end.
The Universe Without an Outside
One of the oldest and most profound questions asks why anything exists at all. Why is there something rather than nothing. A question like this feels simple until we try to answer it. If we say the universe has a cause, then that cause must also have a cause, and we fall into an infinite chain. If we say the universe simply exists by necessity, we define necessity without knowing why it applies.
Part of the problem comes from language that assumes cause is always external. Every event in life has a source that comes before it. The universe, however, includes all that exists. There can be nothing outside the totality. To ask for its cause is to seek something beyond everything.
This paradox resembles the problem of the mind trying to observe its own source. The universe cannot step outside itself any more than the eye can observe itself directly. The question challenges the boundaries of causation and the limits of conceptual thought. The universe might not have a cause in any familiar sense. It might be a starting point that requires no explanation because explanation itself begins within it.
This idea does not remove mystery. It deepens the mystery by showing that we are questioning from inside the thing we are trying to explain.
The Ultimate Unknowable
There are different kinds of limits in knowledge. Some problems cannot be decided by the rules of a system. Other problems cannot be solved by any procedure no matter how long we wait. Some truths are hidden behind horizons that physics prevents us from crossing. These limits are serious but still definable.
The ultimate unknowable belongs to a different category. It refers to whatever cannot be expressed as a question. It cannot be recognized as a thing that is missing because concepts do not apply. It is not that we lack correct vocabulary. It is that no vocabulary can point to what lies there. If mathematics is the language of structure, this is what has no structure.
This idea has a long history in philosophy and theology. It often appears when thinkers confront the notion of the infinite or the source of all existence. Some describe it as darkness, not because it is frightening or evil, but because no light of understanding reaches it.
The ultimate unknowable is the point where explanation loses its subject. It is the place where the edges of meaning dissolve. It is not a failure. It is the natural end of any system that tries to fully grasp the world from within itself.
Learned Ignorance
There are two ways to approach what cannot be known. One is to pretend the limits do not exist and insist that science or logic will eventually answer every question. The other is to recognize that the limit is not a wall blocking progress. It is the horizon that gives shape to the landscape of knowledge.
The medieval thinker Meister Eckhart believed that the only way to understand the divine is to let go of all images of God. Every idea we form makes the infinite into something finite. So we must learn how to unlearn. We must allow the mind to become silent so that the ground of reality can speak without being squeezed into our concepts. This practice does not produce new facts. It changes the attitude of the seeker.
Learned ignorance is humility in the face of mystery. It encourages curiosity without claiming authority. It welcomes wonder as a constant companion. It understands that what we can never know gives meaning to what we can know. It keeps intellect alive by preventing it from turning into arrogance.
At the edge of understanding, silence is not emptiness. It is openness.
The Gift of the Edge
Human beings are defined not only by what we know, but also by what we cannot know. Mathematics gives structure to our perception of reality. It reveals patterns that would otherwise remain invisible. It guides us to places where human thought has never gone before. Yet at each breakthrough, we discover new boundaries that invite us to question further.
The horizon of knowledge is not the limit of existence. It is the limit of our current perspective. Every answer leads to deeper questions. Every discovery expands the circle of mystery. The unknowable is not the enemy of understanding. It is the space where understanding grows.
The metaphor of the eye that cannot see itself captures this spirit beautifully. We are built to encounter mystery. Our limitations are part of our design. We are aware enough to recognize the presence of the unknown even when we cannot step inside it. Consciousness stands on both sides at once, inside the world yet pointed beyond the world.
The universe might be more than mathematics can ever describe. Yet mathematics remains the strongest sign that we are creatures of insight. It is proof that reality welcomes understanding even when it escapes complete description. The search for knowledge becomes a celebration of existence itself.
We live at the edge of knowing. It is a difficult place, but it is also a place of hope. Perhaps the most beautiful truth is the simplest. The horizon is not the end. It is where the sky begins.
Image by Markus Spiske